独学で目指す公務員試験【数的処理】

独学でめざす
公務員試験【数的処理】
公務員試験において、数的処理はとても大事な科目です。受験先を問わず出題があり、しかも出題数も多いため、避けて通ることができません。
にもかかわらず、数的処理は受験生にとって苦手意識を持ちやすい科目のひとつです。
このページでは、公務員試験の中での数的処理の位置づけや、学習のヒントについて紹介していきます。
公務員試験における数的処理の位置づけ
「数的処理」という科目は公務員試験に出会うまでなじみのないものではないでしょうか。教養試験(基礎能力試験)の科目の大半は高校までに学習した科目と重なりますが、数的処理はどの科目からも、「ある程度遠い」もののようです。

数学の知識と重なるところもありますが、純粋な数学というよりは論理的な思考を積み重ねて正解を見つけるところに特徴があります。
だいたい15問前後の出題があり、どの試験であっても数的処理は全問必須解答であるため、この科目が苦手なままだと合格が遠のいてしまいます。にもかかわらず、多くの受験生は公務員試験対策を始めると、「数的処理が難しい・・・」と感じています。
| 一般知能 | 一般知識 | 合 計 出 題 数 |
合 計 回 答 数 |
解 答 時 間 (分) |
||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 数的処理 | 文章理解 | 人文科学 | 自然科学 | 社会科学 | 時 事 |
|||||||||||||||||||
| 数的 推理 |
判断 推理 |
空間 把握 |
資料 解釈 |
現代文 | 英文 | 世界史 | 日本史 | 地理 | 思想 | 文学 芸術 |
数学 | 物理 | 化学 | 生物 | 地学 | 法律 | 政治 | 経済 | 社会 | |||||
| 国家一般職(大卒) | 5 | 6 | 2 | 3 | 6 | 5 | 1 | 1 | 1 | 1 | - | - | 1 | 1 | 1 | - | 1 | 1 | 1 | - | 3 | 40 | 40 | 140 |
| 国税専門官・財務専門官・労働基準監督官 | 6 | 5 | 2 | 3 | 6 | 5 | 1 | 1 | 1 | 1 | - | - | 1 | 1 | - | 1 | 1 | - | 1 | 1 | 3 | 40 | 40 | 140 |
| 裁判所一般職(大卒) | 6 | 7 | 3 | 1 | 5 | 5 | 1 | 1 | 1 | 1 | - | - | 1 | 1 | 1 | 1 | 1 | 3 | 1 | - | - | 40 | 40 | 180 |
| 地方上級 全国型 | 8 | 5 | 3 | 1 | 3 | 5 | 2 | 2 | 2 | - | - | 1 | 1 | 2 | 2 | 1 | 3 | 1 | 3 | 1 | 4 | 50 | 50 | 150 |
| 地方上級 関東型 | 5 | 4 | 2 | 1 | 3 | 5 | 3 | 3 | 3 | - | - | 1 | 1 | 2 | 2 | 1 | 3 | 1 | 4 | 1 | 5 | 50 | 40 | 120 |
| 東京都Ⅰ類B(行政 一般) | 7 | 2 | 4 | 3 | 4 | 4 | 1 | 1 | 1 | - | 1 | - | 1 | 1 | 1 | 1 | 2 | - | 1 | - | 5 | 40 | 40 | 130 |
| 特別区Ⅰ類(事務) | 5 | 6 | 4 | 4 | 5 | 4 | 1 | 1 | 1 | 1 | - | - | 2 | 2 | 2 | 2 | 1 | 2 | 1 | - | 4 | 48 | 40 | 120 |

表の着色部分が数的処理の出題で、だいたい4割くらいの出題を占めていることが多いです。
数的処理は、早めに取り組み始めて「少しずつできるようになっていく」
公務員試験全体にいえることですが、公務員試験では、「得意科目の得意な部分をより伸ばす」より「苦手科目の苦手な部分を克服する」ことに力を入れたほうが得点を伸ばせます。
苦手だからといって、数的処理を苦手にしたまま別の得意科目でその失点分をカバーできるかというと、なかなかうまくいきません。

得意な科目で満点をとれても、出題数の多い数的処理が苦手なままだと、数的処理で失う得点をカバーすることができないのです。
苦手を克服するには、早めに学習に取り掛かり、少しずつ苦手意識を克服していくしかありません。
ただ、具体的に自分が「なんだか前より解けるようになってきたな・・・」という実感を持てないと、学習を続けていくのは難しいでしょう。
そのように前向きな成果を感じながら数的処理を克服していくためのポイントを、次にお伝えします。
独学を意識した公務員試験・数的処理の学習法
(1) 最初は時間をかけて考える
教養試験(基礎能力試験)は時間との戦いになることが多く、試験の直前期には「問題を素早く解く」ことが重要になります。
ただ、少なくとも初めて学習する1巡目においては、問題を解くときの解答時間は意識しなくても大丈夫。むしろ焦って解かずに正解に至るまでのロジックをていねいに追いかけるほうが、上達の近道となります。

どうしても解けない問題については、最初は解説を見てしまってもかまいません。
その代わり解説が、問題のどのようなところに注目して、どのようなルートで正解に至っているかを、よく観察しましょう。
(2) 数的処理では学んだ知識やテクニックを「どう使うか」が求められる
数的処理では、何かしらの知識を「ただ知っている」だけで解ける問題はほとんどなく、それを問題が用意したシチュエーションにうまく当てはめて使うことで、活路を開いていきます。
例えば三平方の定理をきちんと頭で理解していたとしても、問題を見たときに、「いままさに三平方の定理を使える状況が目の前にある」、ということに気づけなければ有効に使えず、問題を解くことができません。
ここに、数的処理という科目の難しさがあります。

問題が提示してくる状況は毎回違うため、全く同じ作業の反復で解けることがなく、がんばって身に付けたことを「正解」というゴールにつなげるために、毎回少しずつ違う「工夫」をしなければならないのです。
では、どうすればよいのか?
(1) 学習方針
数的処理は憲法などの「知識を問う科目」に比べて、「問題を解くことを通じてしか上達しない」度合いが大きい科目です。
逆に、問題を解くために「覚えておくべきこと」は知識科目に比べて圧倒的に少ないですから、
- ❶ 最低限の知識やテクニックを頭に入れる
- ❷ さまざまな問題を通じてそれを実践する訓練をとにかく繰り返す
という、正統派といえる方法でしか実力を伸ばすことができません。
とにかく、「簡単な上達法はない」と言い聞かせて、毎日少しずつでも過去問に触れるようにしましょう。
(2) 判断推理・位置関係の問題を解いてみる
では試しに、数的処理の問題を1問考えてみましょう。
「判断推理」は数的処理の中でも数学的な予備知識がほとんど必要なく、論理的に考えを進めていくことで正解を見つけていく科目です。
『公務員試験 ゼロから合格 基本過去問題集
判断推理』から、判断推理の「位置関係」というジャンルの例題を考えてみましょう。
図のような16の部屋からなる4階建てのワンルームマンションがある。ここにA~Hの8人がいずれかの部屋に1人ずつ住んでおり、A~Hの8人が住んでいる以外の部屋は空き部屋となっている。また、各階とも東側から西側に向かって1号室、2号室、3号室、4号室の部屋番号となっている。このワンルームマンションについて次のア~オが分かっているとき、これらから確実にいえるのはどれか。
- ア 1階には3人が住んでおり、3階と4階には2人ずつが住んでいる。
- イ Aは1階の1号室に住んでいる。また、他の階の1号室に住んでいる者は2人いる。
- ウ Eの両隣の部屋は空き部屋となっている。また、Bは、Eのすぐ下の部屋に住んでおり、かつDよりも下の階に住んでいる。
- エ Fは4号室に住んでいる。また、2号室に住んでいるのはDだけである。
- オ CとEは同じ階に住んでいる。また、GはDよりも下の階に住んでいる。
- 1 AとHは同じ階に住んでいる
- 2 BとCは同じ階に住んでいる。
- 3 Cは4階に住んでいる。
- 4 GはEのすぐ下の階に住んでいる。
- 5 Hは1号室に住んでいる。
まず、この問題のどのようなところに注目すべきかについて、本のアドバイスを見てみましょう。

このタイプの問題は、だいたい同じような解き方で正解にたどり着くことができますので、これから紹介する考えの進め方を身に付けるようにしましょう。
この問題を解くのに知識は必要ありません。ただ、「こういう解き方を覚えておきましょう」というのがあるだけです。
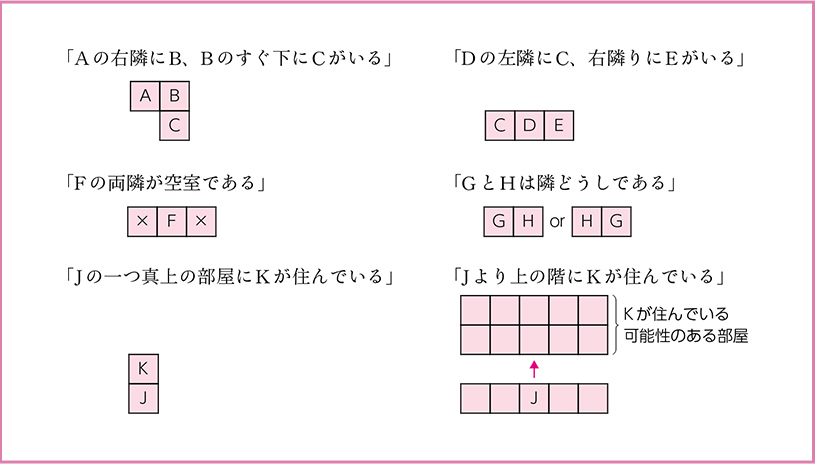
しいていえば、部屋どうしの関係を自分で余白に整理することになるのですが、このとき次のように表します。
(3) 条件からわかることを整理する
最初にすることは、問題文や条件ア~オからわかることを整理していくことです。
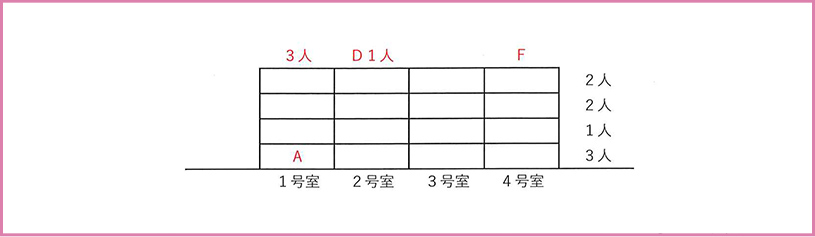
部屋は全部で16部屋あり、住人はA~Hの8人ですから、人が住んでいる部屋が8部屋、空き部屋が8部屋になることがわかります。また、アの条件は2階の住人の人数について述べていませんが、8人のうち7人が1・3・4階に住んでいることがわかるので、残る2階の住人は1人であることがわかります。

このように、与えられた条件では直接示されていないことをうまく見つけることもポイントのひとつです。
この時点で、次のように図に各階の人数を書き込んでしまうとよいでしょう。

また、イの条件からAの部屋がわかり、Aと合わせて1号室には3人が住んでいることがわかります。
さらに、エの条件からFは階がわからないものの4号室に住んでおり、Dも階がわからないものの2号室に住んでいることがわかります。また、2号室に住んでいるのはD1人だということもわかります。
ここまでを書き足すと、次のようになります。
次にウの条件を考えましょう。Eが何階かはわかりませんが、両隣が空き部屋なのでこれを「×」で表すと、

という3部屋の並びが、必ずどこかに当てはまることがわかります。また、BがEのすぐ下の部屋であるため、これにさらに次のように書き足すことができます。

さらにオの条件を見るとCとEが同じ階だとわかりますが、CがEから見てどちら側に位置するかで、次の2通りの可能性が出てきます。
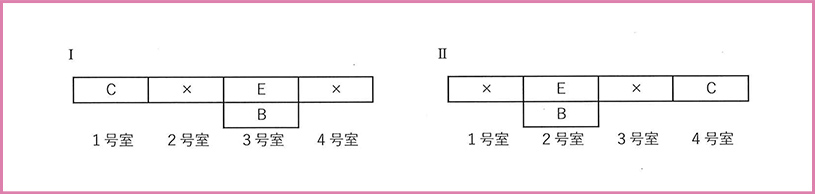
IはCが1号室、EとBが3号室のパターン、ⅡはEとBが2号室、Cが4号室のパターンです。
ここでいったん2通り出てきて「めんどくさいな・・・」と思うかもしれませんが、問題ありません。このうちひとつは、すぐにあり得ないケースとして排除することができます。
というのは、エの条件に基づいて図に書き込んでおいたとおり、2号室の住人はD1人だけです。
ⅡのパターンはEとBの2人が2号室に住んでいるためエの条件に反し、あり得ません。こうして、Iのパターンだけが正解に続く道のりであることがわかります。

検討中に、このように複数の可能性に枝分かれすることがあります。どこかで矛盾が出てきたら、その可能性は「間違いだった」と切り捨てて、残った可能性を検討すればよいのです。
最後に、ウの条件から、DがC、E、Bより上の階に住んでいることがわかり、オの条件から、GがDよりも下の階に住んでいることがわかるので、これも次のように整理しておきます。
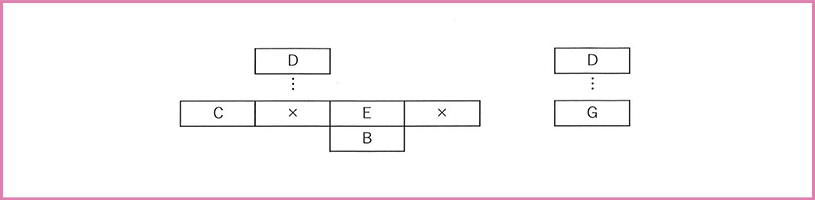
(4) わかったことを利用して推理を進める
条件から読み取れることはこれで全部であり、ここからはこれを手がかりにそれぞれの住人の部屋を確定させていきます。
いま、住人どうしの部屋の関係がわかる材料がふたつあります。このとき、より多くの情報を含んでいるものを優先して考えます。感覚的にいえば、住人どうしの部屋の関係をつなげたものが、より「大きなかたまりになっているもの」を優先します。ここでは、左の図から考えを進めます。
これは、「大きなかたまり」のほうが、「当てはめられる可能性」が限られているためです。
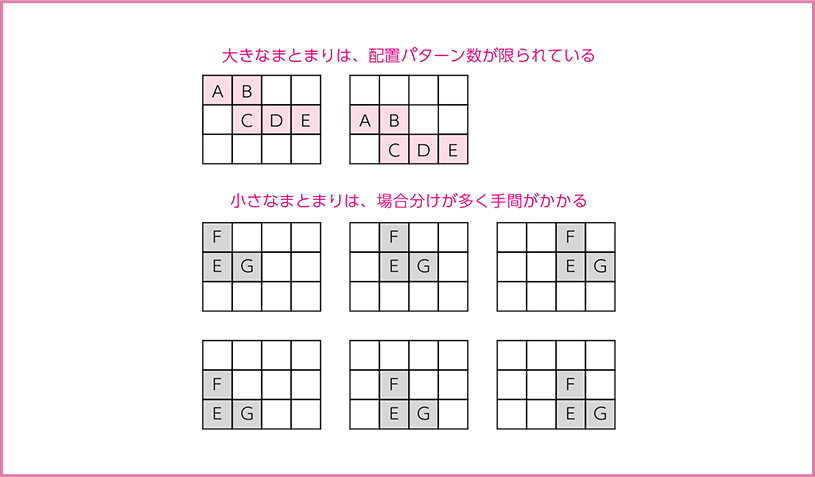
では、CとEと空き部屋ふたつは、マンションの何階に割り当てられるでしょうか?
住人が2人住んでいる階は、3階と4階の2フロアでした。ただ、CとEの住む階より上にDが住んでいることがわかっていますから、Dが4階(の2号室)、CとEが3階に住んでいることが確定します。
すると、Bが自動的に2階の3号室になりますが、2階は1人なので3号室以外は空き部屋だとわかります。同様にDが4階に決まりましたが、2号室に住んでいるのはDだけなので、4階以外の2号室は空き部屋だとわかります。
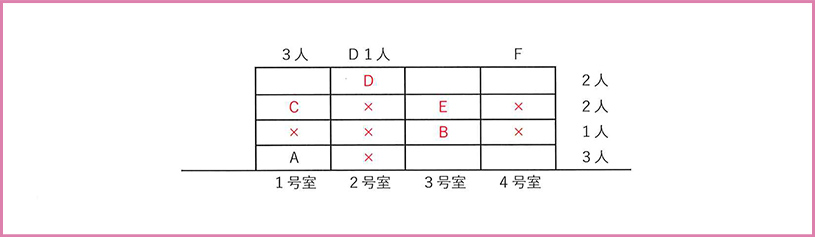
この時点で部屋がわかっていないのは、F、G、Hの3人です。
1号室には3人住んでいることがわかっていますが、いまAとCの2人しか書き込まれていません。空白の4階1号室には、「誰かが住んでいる」ことがわかります。
すると、4階の住人は2人なので、3号室と4号室は空き部屋だとわかります。
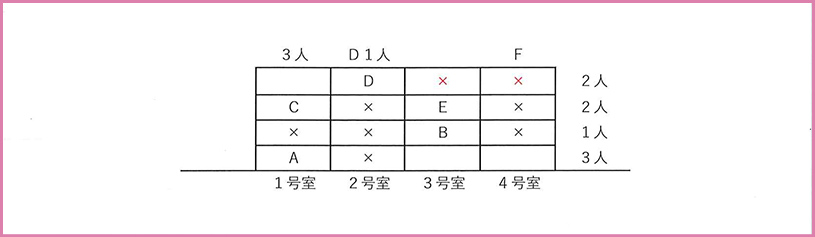
ここまでくればもう一息です。
Fは4号室のどこかに住んでいることがわかっていますが、2~4階の4号室にはすべて空き部屋の「×」が付いてしまったので、Fの部屋は1階4号室に確定します。
また、GはDより下の階に住んでいることだけがわかっていましたが、3階より下でGを当てはめられる部屋は1階3号室だけになったので、ここにGが決まります。
最後に、余った4階1号室にHが入って完成です。
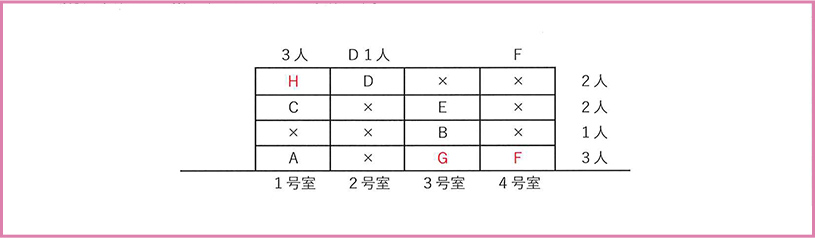
この問題は、これらの部屋の並びから、確実にいえるものを選んで終わりですが、選択肢のうち正しいものを選ぶのは難しくありません。5「Hは1号室に住んでいる。」が正解となります。
このタイプの問題で、慣れないうちに難しいと思うのは、問題文や条件からわかることを漏れなく整理した後、それを組み合わせてわかることを確定していくところです。
はじめは、「CとEを3階に確定できる」と気づくまで、とても時間がかかってしまうかもしれません。
数的処理の学習で少しずつ克服しなければならないのは、まさにこのようなところです。
「CとEが3階だな」とわかるまでの時間は、問題を解けば解くほど確実に短くなっていくはずです。

このとき、解説を読まずに「自分で気づけた」という感覚があるほうが、上達の助けになります。
ですから、最初はどんなに時間がかかってもかまわないので、じっくり考えて解くことを大切にしてみましょう。
独学でめざす公務員試験【数的処理】・まとめ
いかがでしょうか。
数的処理、特に判断推理では、事前に頭に入れておくべき知識は少なく、それをどのように使いこなすかが重要だということがわかると思います。
記事の中で紹介した『公務員試験
ゼロから合格 基本過去問題集
判断推理』には、このほかにも同じような問題が掲載されており、トレーニングを積むことができます。
大切なのは、たくさんの問題に当てはめることのできる「基本的な解法」をきちんと身につけておくこと、また、それを問題の条件に合わせて工夫して使いこなすことです。
少しずつ成果があがってきますから、あきらめずに学習を続けていきましょう!


